An elastic collision is an encounter between two bodies in which the total kinetic energy of the two bodies after the encounter is equal to their total kinetic energy before the encounter. Elastic collisions occur only if there is no net conversion of kinetic energy into other forms.
During the collision of small objects, kinetic energy is first converted to potential energy associated with a repulsive forcebetween the particles (when the particles move against this force, i.e. the angle between the force and the relative velocity is obtuse), then this potential energy is converted back to kinetic energy (when the particles move with this force, i.e. the angle between the force and the relative velocity is acute).
The collisions of atoms are elastic collisions (Rutherford backscattering is one example).
The molecules—as distinct from atoms—of a gas or liquid rarely experience perfectly elastic collisions because kinetic energy is exchanged between the molecules’ translational motion and their internal degrees of freedom with each collision. At any one instant, half the collisions are, to a varying extent, inelastic collisions (the pair possesses less kinetic energy in their translational motions after the collision than before), and half could be described as “super-elastic” (possessing more kinetic energy after the collision than before). Averaged across the entire sample, molecular collisions can be regarded as essentially elastic as long as black-body photons are not permitted to carry away energy from the system.
In the case of macroscopic bodies, perfectly elastic collisions are an ideal never fully realized, but approximated by the interactions of objects such as billiard balls.
When considering energies, possible rotational energy before and/or after a collision may also play a role.
Equations[edit]
One-dimensional Newtonian[edit]
Consider two particles, denoted by subscripts 1 and 2. Let m1 and m2 be the masses, u1 and u2 the velocities before collision, and v1 andv2 the velocities after collision.
The conservation of the total momentum demands that the total momentum before the collision is the same as the total momentum after the collision, and is expressed by the equation
Likewise, the conservation of the total kinetic energy is expressed by the equation
These equations may be solved directly to find vi when ui are known or vice versa. An alternative solution is to first change the frame of reference such that one of the known velocities is zero. The unknown velocities in the new frame of reference can then be determined and followed by a conversion back to the original frame of reference to reach the same result. Once one of the unknown velocities is determined, the other can be found by symmetry.
Solving these simultaneous equations for vi we get:
or
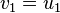
 .
.
The latter is the trivial solution, corresponding to the case that no collision has taken place (yet).
For example:
- Ball 1: mass = 3 kg, velocity = 4 m/s
- Ball 2: mass = 5 kg, velocity = −6 m/s
After collision:
- Ball 1: velocity = −8.5 m/s
- Ball 2: velocity = 1.5 m/s
Property:
Derivation: Using the kinetic energy we can write
Rearrange momentum equation:
Dividing kinetic energy equation by the momentum equation we get:
- the relative velocity of one particle with respect to the other is reversed by the collision
- the average of the momenta before and after the collision is the same for both particles
As can be expected, the solution is invariant under adding a constant to all velocities, which is like using a frame of reference with constant translational velocity.
The velocity of the center of mass does not change by the collision:
The center of mass at time 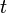 before the collision and at time
before the collision and at time 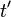 after the collision is given by two equations:
after the collision is given by two equations:
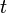 before the collision and at time
before the collision and at time 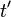 after the collision is given by two equations:
after the collision is given by two equations: , and
, and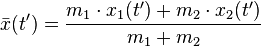
Hence, the velocities of the center of mass before and after the collision are:
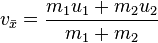 , and
, and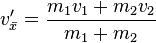
The numerator of  is the total momentum before the collision, and numerator of
is the total momentum before the collision, and numerator of  is the total momentum after the collision. Since momentum is conserved, we have
is the total momentum after the collision. Since momentum is conserved, we have  .
.
 is the total momentum before the collision, and numerator of
is the total momentum before the collision, and numerator of  is the total momentum after the collision. Since momentum is conserved, we have
is the total momentum after the collision. Since momentum is conserved, we have  .
.
With respect to the center of mass both velocities are reversed by the collision: in the case of particles of different mass, a heavy particle moves slowly toward the center of mass, and bounces back with the same low speed, and a light particle moves fast toward the center of mass, and bounces back with the same high speed.
From the equations for  and
and 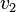 above we see that in the case of a large
above we see that in the case of a large 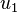 , the value of
, the value of  is small if the masses are approximately the same: hitting a much lighter particle does not change the velocity much, hitting a much heavier particle causes the fast particle to bounce back with high speed.
is small if the masses are approximately the same: hitting a much lighter particle does not change the velocity much, hitting a much heavier particle causes the fast particle to bounce back with high speed.
 and
and 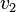 above we see that in the case of a large
above we see that in the case of a large 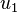 , the value of
, the value of  is small if the masses are approximately the same: hitting a much lighter particle does not change the velocity much, hitting a much heavier particle causes the fast particle to bounce back with high speed.
is small if the masses are approximately the same: hitting a much lighter particle does not change the velocity much, hitting a much heavier particle causes the fast particle to bounce back with high speed.
This is why a neutron moderator (a medium which slows down fast neutrons, thereby turning them into thermal neutrons capable of sustaining a chain reaction) is a material full of atoms with light nuclei (with the additional property that they do not easily absorb neutrons): the lightest nuclei have about the same mass as a neutron.
One-dimensional relativistic[edit]
According to special relativity,
Where p denotes momentum of any particle with mass, v denotes velocity, and c is the speed of light.
In the center of momentum frame where the total momentum equals zero,
Where  represents the rest mass of the first colliding body,
represents the rest mass of the first colliding body, 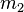 represents the rest mass of the second colliding body,
represents the rest mass of the second colliding body,  represents the initial velocity of the first colliding body,
represents the initial velocity of the first colliding body,  represents the initial velocity of the second colliding body,
represents the initial velocity of the second colliding body, 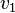 represents the velocity after collision of the first colliding body,
represents the velocity after collision of the first colliding body, 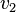 represents the velocity after collision of the second colliding body,
represents the velocity after collision of the second colliding body,  denotes the momentum of the first colliding body,
denotes the momentum of the first colliding body,  denotes the momentum of the second colliding body and
denotes the momentum of the second colliding body and  denotes the speed of light in vacuum,
denotes the speed of light in vacuum, 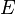 denotes the total energy of the system (i.e. the sum of rest masses and kinetic energies of the colliding bodies).
denotes the total energy of the system (i.e. the sum of rest masses and kinetic energies of the colliding bodies).
 represents the rest mass of the first colliding body,
represents the rest mass of the first colliding body, 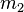 represents the rest mass of the second colliding body,
represents the rest mass of the second colliding body,  represents the initial velocity of the first colliding body,
represents the initial velocity of the first colliding body,  represents the initial velocity of the second colliding body,
represents the initial velocity of the second colliding body, 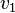 represents the velocity after collision of the first colliding body,
represents the velocity after collision of the first colliding body, 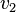 represents the velocity after collision of the second colliding body,
represents the velocity after collision of the second colliding body,  denotes the momentum of the first colliding body,
denotes the momentum of the first colliding body,  denotes the momentum of the second colliding body and
denotes the momentum of the second colliding body and  denotes the speed of light in vacuum,
denotes the speed of light in vacuum, 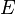 denotes the total energy of the system (i.e. the sum of rest masses and kinetic energies of the colliding bodies).
denotes the total energy of the system (i.e. the sum of rest masses and kinetic energies of the colliding bodies).
Since the total energy and momentum of the system are conserved and the rest masses of the colliding bodies do not change, it is shown that the momentum of the colliding body is decided by the rest masses of the colliding bodies, total energy and the total momentum. The magnitude of the momentum of the colliding body does not change after collision but the direction of movement is opposite relative to the center of momentum frame.
Classical Mechanics is only a good approximation. It will give accurate results when it deals with the object which is macroscopic and running with much lower speed than thespeed of light. Beyond the classical limits, it will give a wrong result. Total momentum of the two colliding bodies is frame-dependent. In the center of momentum frame, according to Classical Mechanics,
It is shown that 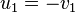 remains true in relativistic calculation despite other differences. One of the postulates in Special Relativity states that the Laws of Physics should be invariant in all inertial frames of reference. That is, if total momentum is conserved in a particular inertial frame of reference, total momentum will also be conserved in any inertial frame of reference, although the amount of total momentum is frame-dependent. Therefore, by transforming from an inertial frame of reference to another, we will be able to get the desired results. In a particular frame of reference where the total momentum could be any,
remains true in relativistic calculation despite other differences. One of the postulates in Special Relativity states that the Laws of Physics should be invariant in all inertial frames of reference. That is, if total momentum is conserved in a particular inertial frame of reference, total momentum will also be conserved in any inertial frame of reference, although the amount of total momentum is frame-dependent. Therefore, by transforming from an inertial frame of reference to another, we will be able to get the desired results. In a particular frame of reference where the total momentum could be any,
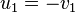 remains true in relativistic calculation despite other differences. One of the postulates in Special Relativity states that the Laws of Physics should be invariant in all inertial frames of reference. That is, if total momentum is conserved in a particular inertial frame of reference, total momentum will also be conserved in any inertial frame of reference, although the amount of total momentum is frame-dependent. Therefore, by transforming from an inertial frame of reference to another, we will be able to get the desired results. In a particular frame of reference where the total momentum could be any,
remains true in relativistic calculation despite other differences. One of the postulates in Special Relativity states that the Laws of Physics should be invariant in all inertial frames of reference. That is, if total momentum is conserved in a particular inertial frame of reference, total momentum will also be conserved in any inertial frame of reference, although the amount of total momentum is frame-dependent. Therefore, by transforming from an inertial frame of reference to another, we will be able to get the desired results. In a particular frame of reference where the total momentum could be any,
We can look at the two moving bodies as one system of which the total momentum is  , the total energy is
, the total energy is 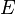 and its velocity
and its velocity  is the velocity of its center of mass. Relative to the center of momentum frame the total momentum equals zero. It can be shown that
is the velocity of its center of mass. Relative to the center of momentum frame the total momentum equals zero. It can be shown that  is given by:
is given by:
 , the total energy is
, the total energy is 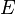 and its velocity
and its velocity  is the velocity of its center of mass. Relative to the center of momentum frame the total momentum equals zero. It can be shown that
is the velocity of its center of mass. Relative to the center of momentum frame the total momentum equals zero. It can be shown that  is given by:
is given by:
Now the velocities before the collision in the center of momentum frame  and
and  are:
are:
 and
and  are:
are:
When  and
and  ,
,
 and
and  ,
, ≈
≈ 
 ≈
≈ 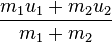
 ≈
≈ 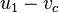 ≈
≈ 
 ≈
≈ 
 ≈
≈ 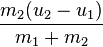
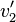 ≈
≈ 
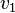 ≈
≈  ≈
≈ 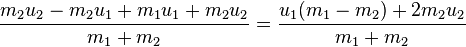
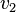 ≈
≈ 
Therefore, the classical calculation holds true when the speed of both colliding bodies is much lower than the speed of light (about 300 million m/s).
Another derivation relativistic formulas for the collision[edit]
We express the so-called parameter of velocity  :
:
 :
:
hence we get
Relativistic energy and momentum are expressed as follows:
Equations sum of energy and momentum colliding masses 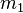 and
and  , (velocities
, (velocities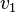 ,
, 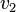 ,
,  ,
,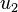 correspond to the velocity parameters
correspond to the velocity parameters  ,
, 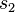 ,
,  ,
, 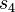 ), after dividing by adequate power
), after dividing by adequate power  are as follows:
are as follows:
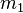 and
and  , (velocities
, (velocities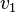 ,
, 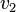 ,
,  ,
,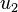 correspond to the velocity parameters
correspond to the velocity parameters  ,
, 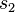 ,
,  ,
, 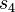 ), after dividing by adequate power
), after dividing by adequate power  are as follows:
are as follows:
and dependent equation, the sum of above equations:
subtract squares both sides equations "momentum" from "energy" and use the identity 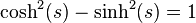 , after simplicity we get:
, after simplicity we get:
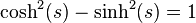 , after simplicity we get:
, after simplicity we get:
for non-zero mass, we get:
as functions  is even we get two solutions:
is even we get two solutions:
 is even we get two solutions:
is even we get two solutions:
from the last equation, leading to a non-trivial solution, we solve 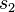 and substitute into the dependent equation, we obtain
and substitute into the dependent equation, we obtain  and then
and then 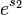 , we have:
, we have:
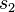 and substitute into the dependent equation, we obtain
and substitute into the dependent equation, we obtain  and then
and then 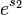 , we have:
, we have:
It is a solution to the problem, but expressed by the parameters of velocity. Return substitution to get the solution for velocities is:
Substitute the previous solutions and replace: 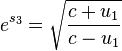 and
and  , after long transformation, with substituting:
, after long transformation, with substituting:  we get:
we get:
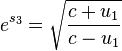 and
and  , after long transformation, with substituting:
, after long transformation, with substituting:  we get:
we get:Two- and three-dimensional[edit]
For the case of two colliding bodies in two dimensions, the overall velocity of each body must be split into two perpendicular velocities: one tangent to the common normal surfaces of the colliding bodies at the point of contact, the other along the line of collision. Since the collision only imparts force along the line of collision, the velocities that are tangent to the point of collision do not change. The velocities along the line of collision can then be used in the same equations as a one-dimensional collision. The final velocities can then be calculated from the two new component velocities and will depend on the point of collision. Studies of two-dimensional collisions are conducted for many bodies in the framework of a two-dimensional gas.
In a center of momentum frame at any time the velocities of the two bodies are in opposite directions, with magnitudes inversely proportional to the masses. In an elastic collision these magnitudes do not change. The directions may change depending on the shapes of the bodies and the point of impact. For example, in the case of spheres the angle depends on the distance between the (parallel) paths of the centers of the two bodies. Any non-zero change of direction is possible: if this distance is zero the velocities are reversed in the collision; if it is close to the sum of the radii of the spheres the two bodies are only slightly deflected.
Assuming that the second particle is at rest before the collision, the angles of deflection of the two particles,  and
and  , are related to the angle of deflection
, are related to the angle of deflection  in the system of the center of mass by[1]
in the system of the center of mass by[1]
 and
and  , are related to the angle of deflection
, are related to the angle of deflection  in the system of the center of mass by[1]
in the system of the center of mass by[1]
The velocities of the particles after the collision are:
Two-Dimensional Collision With Two Moving Objects[edit]
The final x and y velocities of the first ball can be calculated as:[2]
where v1 and v2 are the scalar sizes of the two original speeds of the objects, m1 and m2 are their masses, θ1 and θ2 are their movement angles, that is, 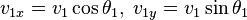 (meaning moving directly down to the right is either a -45° angle, or a 315°angle), and lowercase phi (φ) is the contact angle. (To get the x and y velocities of the second ball, one needs to swap all the '1' subscripts with '2' subscripts.)
(meaning moving directly down to the right is either a -45° angle, or a 315°angle), and lowercase phi (φ) is the contact angle. (To get the x and y velocities of the second ball, one needs to swap all the '1' subscripts with '2' subscripts.)
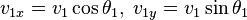 (meaning moving directly down to the right is either a -45° angle, or a 315°angle), and lowercase phi (φ) is the contact angle. (To get the x and y velocities of the second ball, one needs to swap all the '1' subscripts with '2' subscripts.)
(meaning moving directly down to the right is either a -45° angle, or a 315°angle), and lowercase phi (φ) is the contact angle. (To get the x and y velocities of the second ball, one needs to swap all the '1' subscripts with '2' subscripts.)
This equation is derived from the fact that the interaction between the two bodies is easily calculated along the contact angle, meaning the velocities of the objects can be calculated in one dimension by rotating the x and y axis to be parallel with the contact angle of the objects, and then rotated back to the original orientation to get the true x and y components of the velocities.
In an angle-free representation, the changed velocities are computed using the centers x1 and x2 at the time of contact as



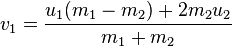
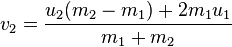
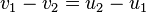













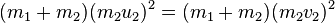

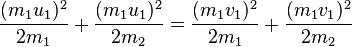
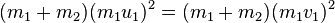
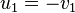
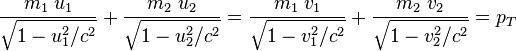



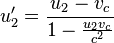

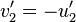
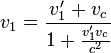
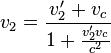

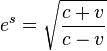
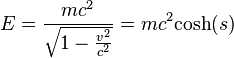




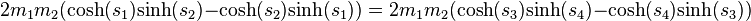


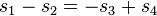
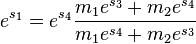






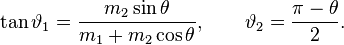
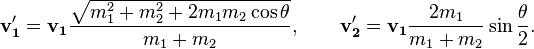
![\begin{align}
v'_{1x}&=\frac{v_{1}\cos(\theta_1-\varphi)(m_1-m_2)+2m_2v_{2}\cos(\theta_2-\varphi)}{m_1+m_2}\cos(\varphi)
\\[0.2em]
&\quad+v_{1}\sin(\theta_1-\varphi)\cos(\varphi+\frac{\pi}{2})
\\[0.8em]
v'_{1y}&=\frac{v_{1}\cos(\theta_1-\varphi)(m_1-m_2)+2m_2v_{2}\cos(\theta_2-\varphi)}{m_1+m_2}\sin(\varphi)
\\[0.2em]
&\quad+v_{1}\sin(\theta_1-\varphi)\sin(\varphi+\frac{\pi}{2})
\end{align}](http://upload.wikimedia.org/math/b/0/9/b09d23456a39b81126c36844fdc13582.png)

No comments:
Post a Comment