For applications and consequences of the law, see Electromagnetic induction.
| Electromagnetism |
|---|
 |
Faraday's law of induction is a basic law of electromagnetism predicting how a magnetic field will interact with an electric circuit to produce an electromotive force (EMF)—a phenomenon called electromagnetic induction. It is the fundamental operating principle of transformers,inductors, and many types of electrical motors, generators and solenoids.[1][2]
The Maxwell–Faraday equation is a generalization of Faraday's law, and forms one of Maxwell's equations.
History[edit]
Electromagnetic induction was discovered independently by Michael Faraday in 1831 and Joseph Henry in 1832.[4] Also, Faraday was the first to publish the results of his experiments.[5][6] In Faraday's first experimental demonstration of electromagnetic induction (August 29, 1831[7]), he wrapped two wires around opposite sides of an iron ring or "torus" (an arrangement similar to a modern toroidal transformer). Based on his assessment of recently discovered properties of electromagnets, he expected that when current started to flow in one wire, a sort of wave would travel through the ring and cause some electrical effect on the opposite side. He plugged one wire into a galvanometer, and watched it as he connected the other wire to a battery. Indeed, he saw a transient current (which he called a "wave of electricity") when he connected the wire to the battery, and another when he disconnected it.[8] This induction was due to the change in magnetic flux that occurred when the battery was connected and disconnected.[3] Within two months, Faraday had found several other manifestations of electromagnetic induction. For example, he saw transient currents when he quickly slid a bar magnet in and out of a coil of wires, and he generated a steady (DC) current by rotating a copper disk near the bar magnet with a sliding electrical lead ("Faraday's disk").[9]
Michael Faraday explained electromagnetic induction using a concept he called lines of force. However, scientists at the time widely rejected his theoretical ideas, mainly because they were not formulated mathematically.[10] An exception was James Clerk Maxwell, who used Faraday's ideas as the basis of his quantitative electromagnetic theory.[10][11][12] In Maxwell's papers, the time-varying aspect of electromagnetic induction is expressed as a differential equation which Oliver Heaviside referred to as Faraday's law even though it is different from the original version of Faraday's law, and does not describe motional EMF. Heaviside's version (see Maxwell–Faraday equation below) is the form recognized today in the group of equations known as Maxwell's equations.
Lenz's law, formulated by Heinrich Lenz in 1834, describes "flux through the circuit", and gives the direction of the induced EMF and current resulting from electromagnetic induction (elaborated upon in the examples below).
Faraday's law[edit]
Qualitative statement[edit]
The most widespread version of Faraday's law states:
This version of Faraday's law strictly holds only when the closed circuit is a loop of infinitely thin wire,[16] and is invalid in other circumstances as discussed below. A different version, the Maxwell–Faraday equation (discussed below), is valid in all circumstances.
Quantitative[edit]
Faraday's law of induction makes use of the magnetic flux ΦB through a hypothetical surface Σ whose boundary is a wire loop. Since the wire loop may be moving, we write Σ(t) for the surface. The magnetic flux is defined by a surface integral:
where dA is an element of surface area of the moving surface Σ(t), B is the magnetic field (also called "magnetic flux density"), and B·dA is a vector dot product (the infinitesimal amount of magnetic flux). In more visual terms, the magnetic flux through the wire loop is proportional to the number of magnetic flux lines that pass through the loop.
When the flux changes—because B changes, or because the wire loop is moved or deformed, or both—Faraday's law of induction says that the wire loop acquires an EMF, 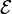 , defined as the energy available from a unit charge that has travelled once around the wire loop.[16][17][18][19] Equivalently, it is the voltage that would be measured by cutting the wire to create an open circuit, and attaching avoltmeter to the leads.
, defined as the energy available from a unit charge that has travelled once around the wire loop.[16][17][18][19] Equivalently, it is the voltage that would be measured by cutting the wire to create an open circuit, and attaching avoltmeter to the leads.
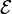 , defined as the energy available from a unit charge that has travelled once around the wire loop.[16][17][18][19] Equivalently, it is the voltage that would be measured by cutting the wire to create an open circuit, and attaching avoltmeter to the leads.
, defined as the energy available from a unit charge that has travelled once around the wire loop.[16][17][18][19] Equivalently, it is the voltage that would be measured by cutting the wire to create an open circuit, and attaching avoltmeter to the leads.
Faraday's law states that the EMF is also given by the rate of change of the magnetic flux:
 ,
,
where 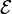 is the electromotive force (EMF) and ΦB is the magnetic flux. The direction of the electromotive force is given by Lenz's law.
is the electromotive force (EMF) and ΦB is the magnetic flux. The direction of the electromotive force is given by Lenz's law.
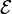 is the electromotive force (EMF) and ΦB is the magnetic flux. The direction of the electromotive force is given by Lenz's law.
is the electromotive force (EMF) and ΦB is the magnetic flux. The direction of the electromotive force is given by Lenz's law.
For a tightly wound coil of wire, composed of N identical turns, each with the same ΦB, Faraday's law of induction states that[20][21]
where N is the number of turns of wire and ΦB is the magnetic flux through a single loop.
Maxwell–Faraday equation[edit]
The Maxwell–Faraday equation is a generalisation of Faraday's law that states that a time-varying magnetic field is always accompanied by a spatially-varying, non-conservative electric field, and vice-versa. The Maxwell–Faraday equation is
(in SI units) where 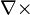 is the curl operator and again E(r, t) is the electric field and B(r, t) is the magnetic field. These fields can generally be functions of position r and time t.
is the curl operator and again E(r, t) is the electric field and B(r, t) is the magnetic field. These fields can generally be functions of position r and time t.
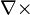 is the curl operator and again E(r, t) is the electric field and B(r, t) is the magnetic field. These fields can generally be functions of position r and time t.
is the curl operator and again E(r, t) is the electric field and B(r, t) is the magnetic field. These fields can generally be functions of position r and time t.
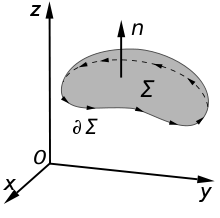
The Maxwell–Faraday equation is one of the four Maxwell's equations, and therefore plays a fundamental role in the theory of classical electromagnetism. It can also be written in an integral form by the Kelvin-Stokes theorem:[22]
where, as indicated in the figure:
- Σ is a surface bounded by the closed contour ∂Σ,
- E is the electric field, B is the magnetic field.
- dℓ is an infinitesimal vector element of the contour ∂Σ,
- dA is an infinitesimal vector element of surface Σ. If its direction is orthogonal to that surface patch, the magnitude is the area of an infinitesimal patch of surface.
Both dℓ and dA have a sign ambiguity; to get the correct sign, the right-hand rule is used, as explained in the article Kelvin-Stokes theorem. For a planar surface Σ, a positive path element dℓ of curve ∂Σ is defined by the right-hand rule as one that points with the fingers of the right hand when the thumb points in the direction of the normal n to the surface Σ.
The integral around ∂Σ is called a path integral or line integral.
Notice that a nonzero path integral for E is different from the behavior of the electric field generated by charges. A charge-generated E-field can be expressed as the gradient of ascalar field that is a solution to Poisson's equation, and has a zero path integral. See gradient theorem.
The integral equation is true for any path ∂Σ through space, and any surface Σ for which that path is a boundary.
If the path Σ is not changing in time, the equation can be rewritten:
The surface integral at the right-hand side is the explicit expression for the magnetic flux ΦB through Σ.
Proof of Faraday's law[edit]
The four Maxwell's equations (including the Maxwell–Faraday equation), along with the Lorentz force law, are a sufficient foundation to derive everything in classical electromagnetism.[16][17] Therefore it is possible to "prove" Faraday's law starting with these equations.[23][24] Click "show" in the box below for an outline of this proof. (In an alternative approach, not shown here but equally valid, Faraday's law could be taken as the starting point and used to "prove" the Maxwell–Faraday equation and/or other laws.)
[show]Outline of proof of Faraday's law from Maxwell's equations and the Lorentz force law.
"Counterexamples" to Faraday's law[edit]
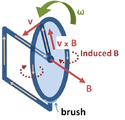
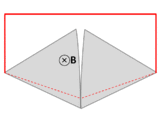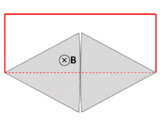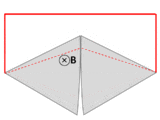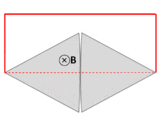
Although Faraday's law is always true for loops of thin wire, it can give the wrong result if naively extrapolated to other contexts.[16] One example is the homopolar generator(above left): A spinning circular metal disc in a homogeneous magnetic field generates a DC (constant in time) EMF. In Faraday's law, EMF is the time-derivative of flux, so a DC EMF is only possible if the magnetic flux is getting uniformly larger and larger perpetually. But in the generator, the magnetic field is constant and the disc stays in the same position, so no magnetic fluxes are growing larger and larger. So this example cannot be analyzed directly with Faraday's law.
Another example, due to Feynman,[16] has a dramatic change in flux through a circuit, even though the EMF is arbitrarily small. See figure and caption above right.
In both these examples, the changes in the current path are different from the motion of the material making up the circuit. The electrons in a material tend to follow the motion of the atoms that make up the material, due to scattering in the bulk and work function confinement at the edges. Therefore, motional EMF is generated when a material's atoms are moving through a magnetic field, dragging the electrons with them, thus subjecting the electrons to the Lorentz force. In the homopolar generator, the material's atoms are moving, even though the overall geometry of the circuit is staying the same. In the second example, the material's atoms are almost stationary, even though the overall geometry of the circuit is changing dramatically. On the other hand, Faraday's law always holds for thin wires, because there the geometry of the circuit always changes in a direct relationship to the motion of the material's atoms.
Although Faraday's law does not apply to all situations, the Maxwell–Faraday equation and Lorentz force law are always correct and can always be used directly.[16]
Both of the above examples can be correctly worked by choosing the appropriate path of integration for Faraday's law. Outside of context of thin wires, the path must never be chosen to go through the conductor in the shortest direct path. This is explained in detail in "The Electromagnetodynamics of Fluid" by W. F. Hughes and F. J. Young, John Wiley Inc. (1965).
Faraday's law and relativity[edit]
Two phenomena[edit]
Some physicists have remarked that Faraday's law is a single equation describing two different phenomena: the motional EMF generated by a magnetic force on a moving wire (see Lorentz force), and the transformer EMF generated by an electric force due to a changing magnetic field (due to the Maxwell–Faraday equation).
James Clerk Maxwell drew attention to this fact in his 1861 paper On Physical Lines of Force. In the latter half of Part II of that paper, Maxwell gives a separate physical explanation for each of the two phenomena.
A reference to these two aspects of electromagnetic induction is made in some modern textbooks.[26] As Richard Feynman states:[16]
Einstein's view[edit]
Reflection on this apparent dichotomy was one of the principal paths that led Einstein to develop special relativity:





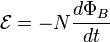
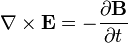


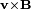 for "circuit moves" and
for "circuit moves" and 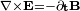 for "field changes".
for "field changes".
No comments:
Post a Comment